Analyzing Hive ransomware
Overview
Hive is a ransomware program that first appeared in 2021. Unlike most ransomware, it uses a custom encryption algorithm, which makes it especially challenging to reverse. I’ll be analyzing the first version of Hive, which is written in Golang, though it has since been rewritten in Rust.
This sample was obtained from vx-underground, and its hash is 2f7d37c22e6199d1496f307c676223dda999c136ece4f2748975169b4a48afe5.
Recovering Function Names
Though the sample included symbols for all functions, Binary Ninja is not capable of analyzing Golang symbols by default. However, Mandiant has released a tool called GoReSym that reads symbols from Golang binaries. This tool produces a JSON file containing the names of both standard library and user-defined functions along with the virtual addresses where they appear.
With the symbols recovered, we can then import them into Binary Ninja with the following script.
import json
import binaryninja
from binaryninja.types import Symbol
from binaryninja.enums import SymbolType
def rename_syms(view):
f = open('/home/remnux/.binaryninja/plugins/gosymtab/syms')
table = json.load(f)
for i in table["UserFunctions"]:
start = i["Start"]
name = i["FullName"]
s = Symbol(SymbolType.FunctionSymbol, int(start), name)
view.define_user_symbol(s)
for i in table["StdFunctions"]:
start = i["Start"]
name = i["FullName"]
s = Symbol(SymbolType.FunctionSymbol, int(start), name)
view.define_user_symbol(s)
for i in table["Types"]:
va = i["VA"]
name = i["Str"]
s = Symbol(SymbolType.DataSymbol, int(va), name)
view.define_user_symbol(s)
binaryninja.plugin.PluginCommand.register("GoReSym integration", "rename functions according to output of GoReSym tool", rename_syms)
With the symbols recovered, the program flow immediately becomes a lot more clear, as the sample uses descriptive names like EncryptFiles and RemoveItself.
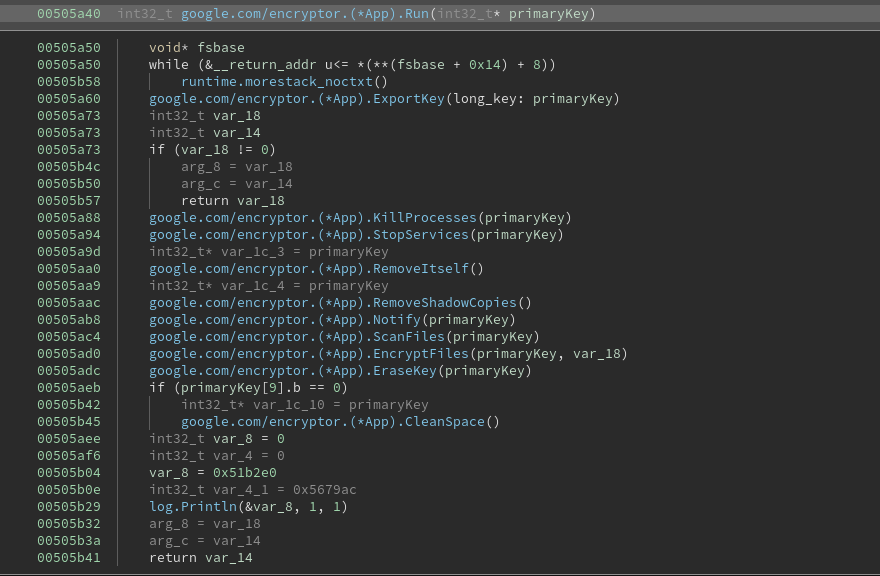
The Primary Key
The encryption algorithm used in this sample relies on a single “primary key”, which is generated by reading 0xa00000 random bytes from the crypto/rand.Read function. As far as I know, Golang’s crypto/rand functions are cryptographically secure, so we have no way to predict what will be generated in this step.
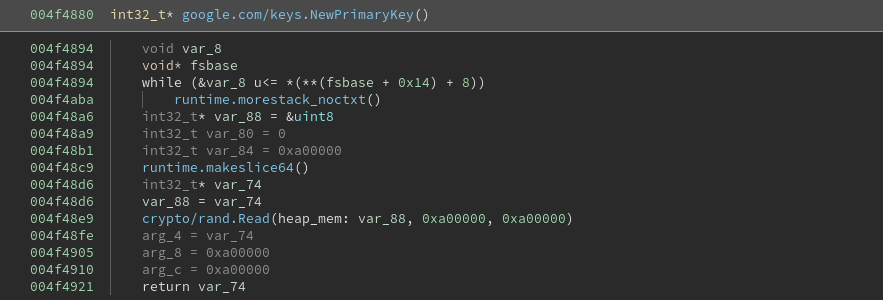
Exporting The Primary Key
Once the primary key is generated, it is encrypted and exported to a file with extension .key.hive. The name of the file is the base64 representation of the MD5 hash of the key.
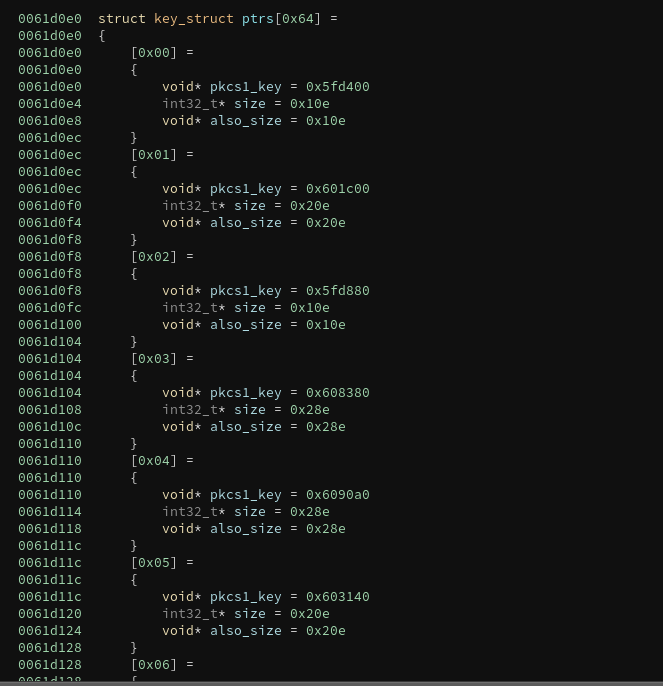
The primary key is divided into blocks, with each block being encrypted by one of several RSA public keys in PKCS1 format. The keys are of varying size, and all of them use the public exponent 65537. The program uses the OAEP encryption scheme with a hash length of 256 for all keys.
There is a table of 100 of these RSA keys hard-coded into the file, and each one is used in order. Once all keys have been used, the program starts over from the beginning of the table.
The RSA-encrypted primary key appears to be the only content of the .key.hive file.
The Encryption Process
The Skipped Bytes
Files are encrypted in blocks of length 0x1000, but a variable length of data is skipped over during encryption.

The length of these skipped segments is chosen differently depending on the size of the file to be encrypted.
The following script can be used to determine how many bytes are skipped:
def get_skip_length(file_length):
if(file_length <= 0x2000): return 0
if(file_length >= 0x20000):
if(file_length >= 0x40000000): m = 1
elif(file_length >= 0x6400000): m = 5
elif(file_length >= 0xa00000): m = 10
elif(file_length >= 0x100000): m = 20
else: m = 30
div_val = m * (file_length >> 0xc) // 100
else: div_val = file_length >> 0xc
return (file_length - (div_val << 0xc)) // (div_val - 1)
In some cases, the number of bytes skipped can be very large, especially for larger file sizes. It might be possible to take advantage of this to recover some data.
The Custom Algorithm
The encryption algorithm begins by randomly selecting two indices from the primary key. The program reads a stream of bytes from the primary key starting from these random indices, and each byte of the plaintext is XORed with the corresponding byte from both streams.

The two random indices can be determined based on the name of the encrypted file. The extension of the encrypted files is a base64 representation of a 32-byte number. The first 16 bytes are the MD5 hash of the primary key, indicating which key should be used for decryption. The second 16 bytes contain both indices concatenated together, represented as 64-bit little-endian integers.
The indices are generated as 64-bit integers, but in order to ensure that they are less than the size of the primary key, the first index is taken modulo 0x900000 and the second index is taken modulo 0x9ffc00.
During encryption, the first key never resets, even when bytes are skipped over during encryption. The second key resets every 0x400 bytes.
My attempt to replicate the encryption algorithm is shown below. This algorithm also functions as a decryption algorithm if the primary key is known, so I tested it by dumping the primary key from memory and using the script to decrypt an encrypted file.
def decrypt_with_primary(primary_name, filename):
primary = open(primary_name, 'rb').read()
ciphertext = open(filename, 'rb').read()
# retrieve indices from base64-encoded strings in filename
base64_str = filename.split('.')[1]
short_key_bytes = base64.b64decode(base64_str + '==')[16:]
key1 = short_key_bytes[0:8]
key2 = short_key_bytes[8:16]
# xor keys are offsets in the primary key
idx1 = int.from_bytes(key1, 'little') % 0x900000
idx2 = int.from_bytes(key2, 'little') % 0x9ffc00
plaintext = b''
# in larger files, leave some data unencrypted
if(len(ciphertext) >= 0x2000):
skip_len = (len(ciphertext) % 0x1000) // (len(ciphertext) // 0x1000 - 1)
else: skip_len = 0
block_len = 0x1000 + skip_len
for j in range(len(ciphertext) // block_len + 1):
pos = block_len*j
for i in range(pos, max(pos+0x1000, len(ciphertext))):
plain = xor(xor(ciphertext[i], primary[idx1 + i]), primary[idx2 + i%0x400])
plaintext += plain
plaintext += ciphertext[pos+0x1000:pos+block_len]
return plaintext
Final Thoughts
Unfortunately, I haven’t yet been able to write a decryptor for this sample. There doesn’t seem to be any trace of the primary key left on the system after encryption is complete - the .key.hive file is RSA encrypted, and the encrypted files contain no relevant information about the primary key.
My first thought was to use some kind of known-plaintext attack, but that’s unlikely to work very well, as each file is encrypted using two different offsets of the primary key. XORing the known plaintext with the encrypted data would give us the XOR of two indices of the primary key, but it’s highly unlikely that the same two indices were ever used to encrypt more than one file.
Strictly speaking, you wouldn’t necessarily need your known plaintext to use the exact same two indices as the encrypted file. Suppose you know that a byte in the ciphertext was XORed with indices A and B, so you need to know A XOR B. If you have a known plaintext that was XORed with index A and some other index C, then you know A XOR C. If you have another known plaintext that uses indices B and C, then you know B XOR C. This means you could recover the key you need by taking (A XOR C) XOR (B XOR C). In this way, you might be able to recover some data by “chaining together” keys from several known plaintexts.
However, this strategy would likely be impractical in the vast majority of cases. You would need a huge amount of known plaintext in order to have a chance at getting the combination of indices you need. Additionally, you’d likely have to XOR thousands of known plaintexts together each time you needed to recover a key, so this method might only be a marginal improvement over brute force.